[skip-to-content]

Sección 5.4 Sistemas de Ecuaciones Lineales I (Introducción)

Definición 5.4.1.
Un sistema de ecuaciones lineales de \(m\) ecuaciones y \(n\) variables es una lista de ecuaciones de la forma
\begin{equation*} \begin{cases} a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n}=b_{1},\\ a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n}=b_{2},\\ \,\,\,\,\,\, \,\,\,\,\,\, \,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\, \vdots \\ a_{m1}x_{1}+a_{m2}x_{2}+...+a_{mn}x_{n}=b_{m}, \end{cases} \end{equation*}
con \(a_{ij},b_{i}\in F\) fijos. Adicionalmente, \(x_{j}\in F\) es variable. Lo anterior puede reescribirse de manera matricial. Es decir
\begin{equation*} \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ & \,\,\,\,\,\, \,\,\,\,\vdots &\\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix}\begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{pmatrix}=\begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \\ \end{pmatrix}. \end{equation*}

O de manera más sencilla: \(A\vec{x}=\vec{b}\text{;}\) con \(A\in \mathcal{M}_{m\times n}(F)\text{,}\) \(\vec{x}\in \mathcal{M}_{n\times 1}(F)\) y \(\vec{b}\in \mathcal{M}_{m\times 1}(F)\text{.}\)

Definición 5.4.2.
Una solución del sistema lineal de ecuaciones \(A\vec{x}=\vec{b}\) es un vector columna
\begin{equation*} \vec{x}=\begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{pmatrix}\in \mathcal{M}_{n\times 1}(F), \end{equation*}
de elementos en el cuerpo \(F\) que satisfacen cada ecuación que compone el sistema.
Considere el siguiente sistema de ecuaciones lineales que dispone de dos ecuaciones y tres incognitas.
\begin{equation*} \begin{pmatrix} 1 & 2 & 3 \\ -2 & 2 & 2 \\ \end{pmatrix}\begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}=\begin{pmatrix} 5 \\ -2 \\ \end{pmatrix}. \end{equation*}
Una solución a este sistema está dada por el vector columna \(\vec{x}\in \mathcal{M}_{3\times 1}(F)\text{,}\) tal que
\begin{equation*} \vec{x}=\begin{pmatrix} 2 \\ 0\\ 1\\ \end{pmatrix}. \end{equation*}

Esto, pues basta realizar la multiplicación de matrices correspondientes; para evidenciar que

\begin{equation*} \begin{pmatrix} 1 & 2 & 3 \\ -2 & 2 & 2 \\ \end{pmatrix}\begin{pmatrix} 2 \\ 0 \\ 1 \\ \end{pmatrix}=\begin{pmatrix} 5 \\ -2 \\ \end{pmatrix}. \end{equation*}
Observación 5.4.4.
Un sistema lineal de ecuaciones (de la Definición 5.4.1) puede poseer tres tipos de soluciones (no son simultaneas):
  1. Solución única.
  2. Soluciones infinitas.
  3. Sin solución.
Observación 5.4.5.

Los sistemas de ecuaciones lineales pueden interpretarse de manera geométrica.

De la Definición 5.4.1, si \(m=n=2\text{;}\) se tendrá un sistema de orden \(2\times 2\text{.}\) Es decir, de dos incognitas y ecuaciones. Tal sistema, es de la forma

\begin{equation*} a_{11}x_{1}+a_{12}x_{2}=b_{1}, \end{equation*}
\begin{equation*} a_{21}x_{1}+a_{22}x_{2}=b_{2}. \end{equation*}

De Geometría Análitica, sabemos que \(\ell_{1}:a_{11}x_{1}+a_{12}x_{2}=b_{1}\) y \(\ell_{2}:a_{21}x_{1}+a_{22}x_{2}=b_{2}\) corresponden a dos rectas en \(\mathbb{R}^{2}.\) Dependiendo de las gráficas de ambas rectas, es posible determinar si el sistema en particular tiene solución o no. Se sigue que

  1. \(\ell_{1}\) y \(\ell_{2}\) se intersectan en un solo punto. Esto implica que el sistema posee solución única.
  2. \(\ell_{1}\) y \(\ell_{2}\) son rectas coincidentes ( \(\ell_{1}=\ell_{2}\)). Esto implica que el sistema posee infinitas soluciones.
  3. \(\ell_{1}\) y \(\ell_{2}\) son rectas paralelas. Esto implica que el sistema no posee solución.

¿Cómo resolver un sistema lineal de ecuaciones? Podemos evocar técnicas aprendidas durante la Enseñanza Media (sustitución, reducción o igualación).

Desafortunadamente, dichas estrategias no suelen ser muy efectivas a la hora de trabajar con un sistema de orden \(m\times n\) ( \(m\) incognitas y \(n\) ecuaciones). Sin embargo, pueden emplearse de manera astuta. Considere el Ejemplo 5.4.6.

Considere el sistema lineal de ecuaciones
\begin{equation*} \begin{cases} x-2y+z=0,\,\,\,\, (1)\\ 2y-8z=8,\,\,\,\, (2)\\ -4x+5y+9z=-9.\,\,\,\, (3)\\\end{cases} \end{equation*}

Resolveremos el sistema en cuestión. Se multiplicará por 4 la ecuación (1). De esta forma, se tendrá

\begin{equation*} \begin{cases} 4x-8y+4z=0,\,\,\,\, (1)\\ 2y-8z=8,\,\,\,\, (2)\\ -4x+5y+9z=-9.\,\,\,\, (3)\\\end{cases} \end{equation*}

Sumando (1) y (3), se obtiene

\begin{equation*} \begin{cases} -3y+13z=-9,\,\,\,\, (4)\\ 2y-8z=8.\,\,\,\, (5)\\ \end{cases} \end{equation*}
Multiplicando por \(2\) y \(3\) en las ecuaciones (4) y (5) respectivamente, se obtiene
\begin{equation*} \begin{cases} -6y+26z=-18,\,\,\,\, (6)\\ 6y-24z=24.\,\,\,\, (7)\\ \end{cases} \end{equation*}
Sumando las ecuaciones (6) y (7), se logra \(2z=6\text{.}\) Esto implica que \(z=3\text{.}\)

De (5), se sabe que \(2y-8z=8\text{.}\) Esto implica que \(y=16.\)

Para determinar la variable \(x\text{,}\) se puede reemplazar los valores de \(z\) e \(y\) obtenidos en (1) o (3). En particular, se reemplazará en (1). Por lo tanto

\begin{equation*} x-2(16)+3=0 \Leftrightarrow x=29. \end{equation*}

Note que el vector columna

\begin{equation*} \begin{pmatrix} 29 \\ 16 \\ 3 \\ \end{pmatrix}, \end{equation*}
es la solución del sistema en particular. Esto, pues se verifica la igualdad de matrices
\begin{equation*} \begin{pmatrix} 1 & -2 & 1 \\ 0 & 2 & -2 \\ -4 & 5 & 9 \\ \end{pmatrix}\begin{pmatrix} 29 \\ 16 \\ 3 \\ \end{pmatrix}=\begin{pmatrix} 0 \\ 8 \\ -9 \\ \end{pmatrix}. \end{equation*}

Para resolver el sistema del Ejercicio 5.5.6 se utilizaron las siguientes operaciones:

  1. Multiplicar una ecuación por una constante no nula.
  2. Intercambiar dos ecuaciones.
  3. Sumar a una ecuación un múltiplo de otra ecuación.

Estas técnicas corresponden a las operaciones elementales filas; definidas en la seccíón anterior (Operaciones Elementales Filas y Matrices Escalonadas).

El objetivo del presente capítulo es proporcionar un mecánismo que permita resolver sistemas de ecuaciones lineales recurriendo al mécanismo de operaciones elementales filas (Gauss - Jordan). Pero antes, es necesario introducir el concepto de matriz ampliada.

Definición 5.4.7.
(Matriz Ampliada) Considere el sistema de ecuaciones lineales de \(m\) ecuaciones y \(n\) variables: \(A\vec{x}=\vec{b}\text{,}\) de la Definición 5.4.1.

Se define la matriz ampliada asociada a dicho sistema de ecuaciones, como el arreglo matricial

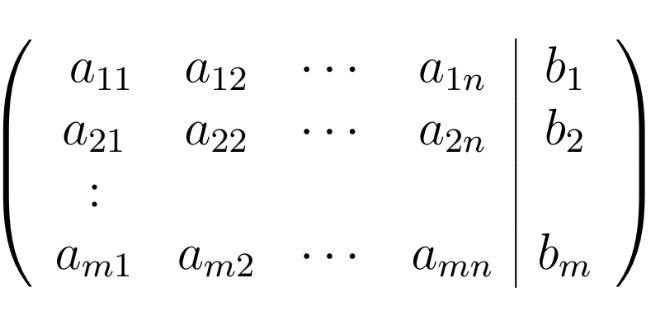
La matriz ampliada asociada al sistema de ecuaciones \(A\vec{x}=\vec{b}\text{,}\) se denotará como \((A:b).\)

Considere el sistema lineal de ecuaciones
\begin{equation*} \begin{cases} 5x-4y-3z=2,\\ 4x+y-z=3,\\ -x-y+z=1. \end{cases} \end{equation*}

La matriz ampliada asociada con el sistema de ecuaciones está dada por

\begin{equation*} \begin{pmatrix} 5 & -4 & -3& :\, 2 \\ 4 & 1 & -2&:\, 3 \\ -1 & -3 & 1&:\, 1 \\ \end{pmatrix} \end{equation*}

A la hora de resolver un sistema de resolver un sistema de ecuaciones lineales mediante Gauss - Jordan (realizar operaciones elementales filas), el uso de la matriz ampliada será clave. Y más aun, pues está involucrada en el Teorema de Rouché - Fröbenius.

login