Sección 1.2 Introducción a la Teoría de Conjuntos
Georg Cantor, padre de la Teoría de Conjuntos (junto a Dedekind y Frege); alude a que el concepto de Conjunto no está definido formalmente, pero -que dependiendo del contexto- es intuitivamente claro y alude a una "colección de objetos".
Ejemplo 1.2.1.
- La colección \(\mathcal{A}= \left\lbrace 2,3,5,7,11,13,17,19,23,...\right\rbrace\) -intuitivamente- es el conjunto de todos los números primos.
- La colección \(\mathcal{B}=\left\lbrace \text{Hiperbola, Elipse, Parábola, Circunferencia}\right\rbrace\) es el conjunto de secciones cónicas.
- La colección \(\mathcal{C}=\left\lbrace x\in \mathbb{R}:x^{2}-5x+6=0\right\rbrace\) es el conjunto es el conjunto solución de la ecuación cuadrática \(x^{2}+5x+6\) en \(\mathbb{R}\text{.}\)
- La colección \(\mathcal{D}=\left\lbrace m\in \mathbb{N}: m\le n \land \text{mcd}(m,n)=1\right\rbrace\) es el conjunto de números naturales menores y coprimos con \(n\text{.}\)
Los objetos que constituyen un conjunto se denominan elementos. Por convención, emplearemos letras mayúsculas para denotar un conjunto y minúsculas para los elementos. Si \(x\) es un elemento de \(\mathcal{S}\text{,}\) entonces \(x\in \mathcal{S}\text{.}\) Si \(x\) no es un elemento de \(\mathcal{S}\text{,}\) entonces \(x\notin \mathcal{S}\) (alternativamente, \(\overline{x\in \mathcal{S}}\)).
Un conjunto \(\mathcal{S}\) puede ser definido por comprensión (exhibiendo una característica de los elementos de \(\mathcal{S}\)) o por extensión (escribiendo explícitamente todos los elementos de \(\mathcal{S}\)).
Ejemplo 1.2.2.
Ejercicio 1.2.3.
Subsección 1.2.1 Igualdad y Subconjunto
Para lo que viene, será importante estar familiarizado con el concepto de proposiciones lógicas y cuantificadores. Considere \(A,B\text{;}\) conjuntos.
Definición 1.2.4.
(Subconjunto o Inclusión): \(A\subseteq B \ \ \Leftrightarrow \ \ \forall \ \ x , \ \ x\in A \Rightarrow x\in B\text{.}\)Es decir, \(A\) es un subconjunto de (o está incluido en) \(B\text{.}\)
Observación 1.2.5.
Si \(A\subseteq B\) y \(A\neq B\text{,}\) entonces \(A \subset B\text{.}\)Es decir, \(A\) es subconjunto propio de \(B\text{.}\)
Definición 1.2.6.
(Igualdad): \(A=B \Leftrightarrow \forall \ \ x , \ \ x\in A \Leftrightarrow x\in B\text{.}\)Es decir; si \(A\) y \(B\) tienen los mismos elementos, entonces son iguales.
Proposición 1.2.7.
(Igualdad e Inclusión) \(A=B \Leftrightarrow A\subseteq B \ \ \land \ \ B\subseteq A\text{.}\)Demostración.
Proposición 1.2.8.
Considere los conjuntos \(A,B,C\text{.}\) Entonces- \(A\subseteq A.\)
- \(A=A.\)
- \(A=B \Leftrightarrow B=A.\)
- \((A=B) \land B=C) \Rightarrow A=C.\)
- \((A\subseteq B \land B\subseteq C) \Rightarrow A\subseteq C.\)
Demostración.
Note que \(\left\lbrace 1,2,3\right\rbrace =\left\lbrace 3,2,1\right\rbrace =\left\lbrace 1,1,1,1,2,3,3\right\rbrace\text{.}\) En conjuntos no importa el orden, ni la cantidad de repeticiones de los elementos.
Subsección 1.2.2 Conjunto Vacío y Universo
Definición 1.2.9.
(Conjunto Vacío) Se define el conjunto vacío comoObservación 1.2.10.
El conjunto vacío no tiene ningún elemento y es único.Observación 1.2.11.
\(\varnothing \subseteq \mathcal{S}\) ( \(\mathcal{S}\) es un conjunto arbitrario).Ejemplo 1.2.12.
Definición 1.2.13.
(Conjunto Universo) Se asumirá la existencia de un conjunto \(U\) (de referencia), en donde viven todos los elementos con los cuales se va a trabajar. ¡El conjunto universo es todo!Ejemplo 1.2.14.
Subsección 1.2.3 Diagramas de Venn
Un diagrama de Venn exhibe de manera grafica la relación lógica existente entre conjuntos. Permite visualizar de manera certera, las relaciones entre conjuntos. Fueron introducidos por el matemático britanico John Venn (ver Figura 1.2.15).
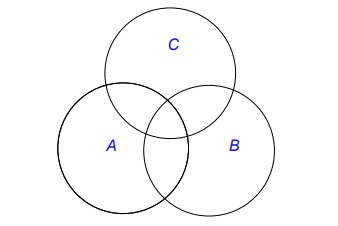
Subsección 1.2.4 Operaciones con Conjuntos
Considere los conjuntos \(A,B,C, U\) (referencial o universo). Definiremos ciertas operaciones entre estos conjuntos, los cuales nos permiten definir nuevas colecciones.
Definición 1.2.16.
(Unión):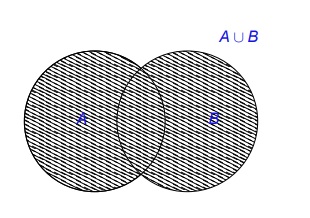
Definición 1.2.18.
(Intersección):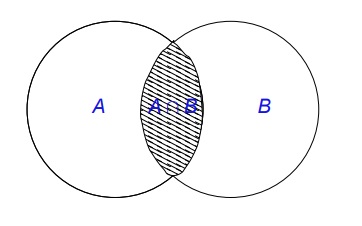
Observación 1.2.20.
Dos conjuntos \(A\) y \(B\) son disjuntos si no tienen elementos en común. Es decir, \(A\cap B=\varnothing\text{.}\)Definición 1.2.21.
(Complemento)\(A^{c}\) denota el complemento de \(A\text{;}\) formado por los elementos que no están en \(A\text{.}\)
Ejemplo 1.2.22.
El complemento de un conjunto, expresado mediante diagramas de Venn está dado por la Figura 1.2.23
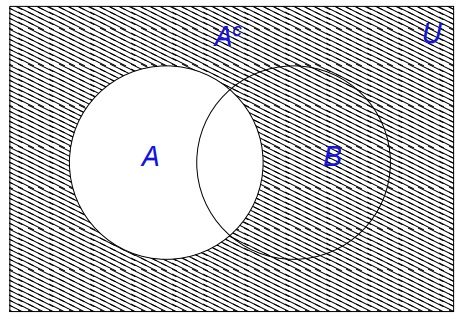
Definición 1.2.24.
(Diferencia):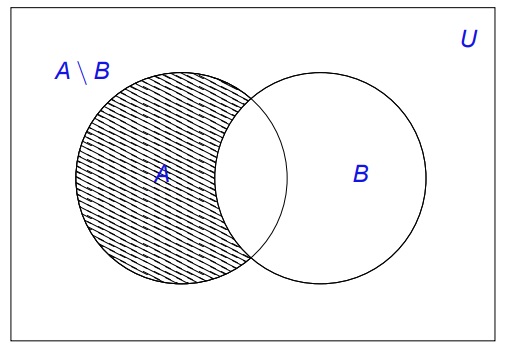
Definición 1.2.26.
(Diferencia Simétrica)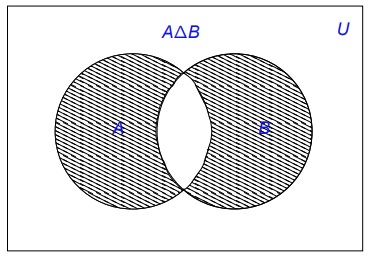
Ejemplo 1.2.28.
- \(A^{c}\cup B^{c} = \left\lbrace 1,4,5,6,7,8 \right\rbrace.\)
- \(B^{c} \backslash C^{c} = \varnothing.\)
- \(A\cap C= \left\lbrace 2\right\rbrace.\)
- \((B\cap C^{c})^{c}= \left\lbrace 2,3,4,5,8 \right\rbrace.\)
- \((A\triangle B)\triangle C = \left\lbrace 2,4,6,7,8 \right\rbrace.\)
A continuación, exhibimos una serie de propiedades sobre operaciones en conjuntos. Nos referimos al Álgebra de Conjuntos. La demostración de estas proposiciones es análoga a las Tautologías Notables (Álgebra de Proposiciones). Considere los conjuntos \(A,B,C\) y \(U\) (de referencia o universal).
- Conmutatividad: \(A\cup B=B\cup A\) y \(A\cap B=B\cap A.\)
- Asociatividad: \(A\cup(B\cup C)=(A\cup B)\cup C\) y \(A\cap(B\cap C)=(A\cap B)\cap C.\)
- Distribuitividad: \(A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\) y \(A\cup (B\cap C)=(A\cup B)\cap (A\cup C).\)
- Idempotencia: \(A\cup A=A\) y \(A\cap A=A .\)
- Identidad: \(A \cup \varnothing = A\text{,}\) \(A\cap \varnothing=\varnothing\text{,}\) \(A\cup U=U\) y \(A\cap U=A.\)
- Del Complemento: \((A^{c})^{c}=A, A\cup A^{c}=U, A\cap A^{c}=\varnothing, U^{c}=\varnothing\) y \(\varnothing^{c}=U.\)
- Absorción: \(A\cap (A\cup B)=A\) y \(A\cup (A\cap B)=A.\)
- Inclusión \((A\cap B) \subseteq A \subseteq (A\cup B)\) y \((A\cap B)\subseteq B\subseteq (A\cup B).\)
- Leyes de De Morgan: \((A\cup B)^{c}=A^{c}\cap B^{c}\) y \((A\cap B)^{c}=A^{c}\cup B^{c} .\)
- De la Diferencia Simétrica: \(A\triangle B=B\triangle A\text{,}\) \((A\triangle B)\triangle C=A\triangle (B\triangle C)\text{,}\) \(A\triangle A=\varnothing\) y \(A\triangle \varnothing=A\text{.}\)
Ejemplo 1.2.29.
Ejercicio 1.2.30.
Podemos construir un diccionario Lógica - Conjunto; el cual muestra la relación entre los conectivos lógicos y las operaciones con conjuntos. Se tiene que
- \(\Rightarrow\) (Lógica) es \(\subseteq\) (Conjuntos).
- \(\Leftrightarrow\) (Lógica) es \(=\) (Conjuntos).
- \(\lor\) (Lógica) es \(\cup\) (Conjuntos).
- \(\land\) (Lógica) es \(\cap\) (Conjuntos).
- \(\veebar\) (Lógica) es \(\triangle\) (Conjuntos).
- \(-\)(Lógica) es \(^{c}\) (Conjuntos).
Subsección 1.2.5 Cardinalidad de un Conjunto
Es natural preguntarse cual es la cantidad de elementos de un conjunto no vacío. Esto nos motiva a introducir el concepto de cardinal de un conjunto.
Definición 1.2.31.
(Cardinal) Sea \(A\text{,}\) un conjunto no vacío. El cardinal de \(A\) es el número de elementos en el conjunto y se denota por \(\left| A\right|\text{.}\)Observación 1.2.32.
Un conjunto \(A\) se dice finito si su cardinal es finito.Nos interesa saber cual es la cardinalidad de \(A\cap B\) y \(A\cup B\text{.}\) Para esto, consideraremos el siguiente resultado (Proposición 1.2.33)
Proposición 1.2.33.
(Propiedades del Cardinal) Sean \(A,B\) y \(C\text{;}\) conjuntos no vacíos y finitos. Entonces- \(\left| \varnothing \right|=0\text{.}\)
- Si \(A \subseteq B\text{,}\) entonces \(\left| B-A \right| =\left| B \right| - \left| A \right|.\)
- \(\left| A \cup B \right| =\left| A \right| +\left| B \right| -\left| A\cap B \right|.\)
- \(\left| A \cup B \cup C \right| =\left| A \right| +\left| B \right|+\left| C \right|+\left| A \cap B \cap C \right| -\left| A \cap B \right|-\left| A \cap C \right|-\left| B \cap C \right|.\)
Subsección 1.2.6 Conjunto Potencia, Particiones y Producto Cartesiano
Definición 1.2.34.
Sea \(\mathcal{S}\) un conjunto. Se denomina conjunto potencia de \(\mathcal{S}\) (y se denota \(\mathcal{P}(\mathcal{S})\)) a la colección de todos los subconjuntos de \(\mathcal{S}\text{.}\) Es decirObservación 1.2.35.
\(\varnothing, \mathcal{S} \subseteq \mathcal{P}(\mathcal{S}).\)Ejemplo 1.2.36.
En efecto
La cantidad de elementos de \(\mathcal{P}(\mathcal{S})\) es \(8\text{.}\) Esto nos motiva a introducir el siguiente resultado (Proposición 1.2.37).
Proposición 1.2.37.
Sea \(\mathcal{S}\) un conjunto con \(n\) elementos. EntoncesEjemplo 1.2.38.
Se sigue que
Ejercicio 1.2.39.
Proposición 1.2.40.
(Propiedades del Conjunto Potencia) Sean \(A,B\text{;}\) conjuntos. Entonces- \(\mathcal{P}(A)\cap \mathcal{P}(B)=\mathcal{P}(A\cap B).\)
- \(\mathcal{P}(A)\cup \mathcal{P}(B)\subseteq \mathcal{P}(A\cup B).\)
Demostración.
En 2, vea que
Ejercicio 1.2.41.
Dado que estamos familiarizados con el conjunto potencia, podemos introducir el concepto de partición.
Definición 1.2.42.
(Partición de Conjuntos) Se dice que \(\mathcal{C}\subseteq \mathcal{P}(A)\) es una partición de \(A\) si- \(\forall \ B \in \mathcal{C}, B\neq \varnothing.\)
- Los elementos de \(\mathcal{C}\) son disjuntos a pares: Para todo \(B,B'\in \mathcal{C}\) tales que \(B \neq B'\text{,}\) entonces \(B \cap B'=\varnothing.\)
- \(\mathcal{C}\) cubre \(A\text{:}\) \(\displaystyle\bigcup_{B \in \mathcal{C}}{B}=A\text{.}\)
Ejemplo 1.2.43.
- \(\left\lbrace \left\lbrace x\right\rbrace, \left\lbrace y\right\rbrace, \left\lbrace z\right\rbrace \right\rbrace.\)
- \(\left\lbrace \left\lbrace x,y\right\rbrace, \left\lbrace z\right\rbrace \right\rbrace.\)
- \(\left\lbrace \left\lbrace x,z\right\rbrace, \left\lbrace y\right\rbrace \right\rbrace.\)
- \(\left\lbrace \left\lbrace x\right\rbrace, \left\lbrace y,z\right\rbrace \right\rbrace.\)
- \(\left\lbrace \left\lbrace x,y,z\right\rbrace \right\rbrace .\)
Ejemplo 1.2.44.
- \(\left\lbrace \left\lbrace x\right\rbrace, \left\lbrace x,y,z\right\rbrace \right\rbrace.\)
- \(\left\lbrace \left\lbrace x\right\rbrace, \left\lbrace y\right\rbrace \right\rbrace.\)
Para introducir el concepto de Producto Cartesiano, será importante recordar que si \((a,b)\) y \((c,d)\) son pares ordenados tales que \((a,b)=(c,d)\) entonces \(a=c\) y \(b=d\text{.}\)
Definición 1.2.45.
(Producto Cartesiano) Sean \(A,B\text{;}\) dos conjuntos no vacíos. Se define el producto cartesiano entre \(A\) y \(B\) comoDe la Definición 1.2.45, se deduce de que los elementos del producto cartesiano entre \(A\) y \(B\) son pares ordenados de la forma \((a,b)\text{;}\) donde la primera componente vive en \(A\text{,}\) mientras que la segunda pertenece a \(B\)
.Note que \((a,b)\) no necesariamente es \((b,a)\text{,}\) por lo que \(A\times B \neq B \times A\) (el producto cartesiano es anticonmutativo).
Proposición 1.2.46.
Sean \(A,B\text{;}\) dos conjuntos no vacíos tales que \(\left| A\right| =n\) y \(\left| A\right| =m\text{.}\) EntoncesEjemplo 1.2.47.
Si \(A\) y \(B\)son conjuntos no vacíos, ¿como es la gráfica de los elementos de un producto cartesiano? Dado que los elementos de \(A\times B\) son pares ordenados, la grafica de estos elementos se realiza en un sistema de coordenadas rectangulares.
Ejemplo 1.2.48.
La gráfica de los elementos de \(P\times Q\) es 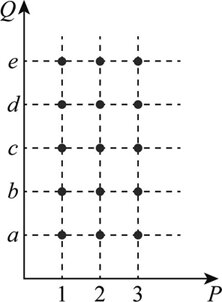
Proposición 1.2.50.
(Propiedades del Producto Cartesiano) Considere los conjuntos no vacíos \(A,B,C,D,X,Y\text{.}\) Entonces- \(A \times B= \varnothing \Leftrightarrow A=\varnothing \lor B=\varnothing.\)
- \(A \subseteq X \land B \subseteq Y \Rightarrow (A \times B) \subseteq (X \times Y).\)
- \(A \times (B\cap C)= (A\times B) \cap (A\times C).\)
- \(A \times (B\cup C)= (A\times B) \cup (A\times C).\)
- \((A \times B) \cap (C \times D)= (A\cap C) \times (B\cap D).\)
- \((A \times B) \cup (C \times D)= (A\cup C) \times (B\cup D).\)
Subsección 1.2.7 Cuantificadores
Para introducir el concepto de cuantificadores, es importante enfatizar de que estos últimos no se emplean con proposiciones lógicas. Se utilizan con "afirmaciones abiertas" denominadas funciones proposicionales. Para tales afirmaciones, carece de sentido preguntarse cual es su valor de verdad.
No obstante; al combinar una función proposiconal con cuantificadores, se obtiene una proposición lógica que posee un valor de verdad.
Ejemplo 1.2.51.
- \(p(x):x\) es mujer.
- \(q(x):x=\pi\text{.}\)
- \(r(x):x\) es un divisor de 20.
- \(s(x,y,z,n):x^n + y^n =z^n\text{.}\)
A continuación, exhibimos los distintos tipos de cuantificadores combinados con funciones proposicionales.
Definición 1.2.52.
(Cuantificador Universal) Sea \(p(x)\) una función proposicional y \(A\) un conjunto. La expresión \((\forall \ x \in A) \ p(x)\) se lee "para todo \(x \in A\text{,}\) se cumple \(p(x)\)". \(\forall\text{,}\) es el cuantificador universal.Ejemplo 1.2.53.
Se debe hacer énfasis de que en presencia del cuantificador universal, basta que un valor \(x \in A\) no cumpla \(p(x)\text{;}\) para que la expresión \((\forall \ x \in A) \ p(x)\) sea falsa.
Ejemplo 1.2.54.
Definición 1.2.55.
(Cuantificador Existencial) Sea \(p(x)\) una función proposicional y \(A\) un conjunto. La expresión \((\exists \ x \in A) \ p(x)\) se lee "existe \(x \in A\text{,}\) tal que se cumple \(p(x)\)". \(\exists\text{,}\) es el cuantificador existencial.Ejemplo 1.2.56.
Se debe hacer énfasis de que en presencia del cuantificador existencial, basta que un valor \(x \in A\) si cumpla \(p(x)\text{;}\) para que la expresión \((\exists \ x \in A) \ p(x)\) sea verdadera.
Ejemplo 1.2.57.
Definición 1.2.58.
(Cuantificador de Existencia y Unicidad) Sea \(p(x)\) una función proposicional y \(A\) un conjunto. La expresión \((\exists ! \ x \in A) \ p(x)\) se lee "existe un único \(x \in A\) tal que se cumple \(p(x)\)". \(\exists !\text{,}\) es el cuantificador de existencia y unicidad.Adicionalmente, el cuantificador de existencia y unicidad se puede definir como
Ejemplo 1.2.59.
Ejemplo 1.2.60.
Definición 1.2.61.
(Negación de Cuantificadores) Sea \(p(x)\) una función proposicional. Se define la negación de los cuantificadores- \(\overline{(\forall \ x \in A) \ p(x)} \Leftrightarrow (\exists \ x \in A) \ \overline{p(x)}.\)
- \(\overline{(\exists \ x \in A) \ p(x)} \Leftrightarrow (\forall \ x \in A) \ \overline{p(x)}.\)
- \(\overline{(\exists ! \ x \in A) \ p(x)} \Leftrightarrow (\forall x \ \overline{p(x)}) \vee [\exists x \ \exists y, (p(x) \wedge p(y) \wedge x\neq y)].\)
Ejemplo 1.2.62.
La función proposicional es falsa, ya que si \(x=0\) entonces no existe ningún \(y\in \mathbb{R}\) tal que \(x\cdot y=4.\) La negación es: